Titanic Dataset: Exploratory Data Analysis, Even More

Published Mon, Jan 31, 2022 by Rick Kochanski

Not sure what to do next. Will likely be some repetition, but…

Age

Going to take another look at Age. Start with a histplot (density plot) for Age, with hue for gender.

In [14]:

age_fs = sns.FacetGrid(k_trn, hue="Survived", height=6).map(sns.histplot, "Age", stat="density", kde=True, linewidth=0).add_legend()

seaborn density histplot for Age with hue on gender showing negative ages

See the problem? It took me some time. And, because of the way I set axes limits for the subsequent KDE plot, it didn’t show the problem.

Well it would appear my attempt to impute missing ages generated negative ages for some of the passengers. That really is not a good thing. So, I went back to the post Titanic Dataset: Missing Data, Part 3 and reworked the imputation. Now seems to have no negative ages. Clearing the output on the related notebook and restarting shows the negative ages are now gone. Now back to this post.

seaborn density histplot for Age with hue on gender without any negative ages

Probability Density Functions (PDFs) are overlapping. So we aren’t going to see any big differences with respect to Age. But, once again we confirm that for passenger’s under the age of 20, it would seem the likelihood of survival was better than that of perishing. Similarly for those between 30 and 40. Nothing new, but confirmed.

Now, Seaborn KDE plots for comparison and coding experience.

In [6]:

sns.set(font_scale=1.5)
fig, ax = plt.subplots(figsize=(30,6))
g = sns.kdeplot(k_trn['Age'][(k_trn['Survived'] == 0)].dropna(), shade=True, color="red")
g = sns.kdeplot(k_trn['Age'][(k_trn['Survived'] == 1)].dropna(), shade=True, color="blue")
_ = g.set(xlim=(0 , k_trn["Age"].max()))
_ =g.legend(['Perished', 'Survived'])
_ =plt.xticks(rotation=25)
_ = ax.set_xlabel("Age", weight='bold')

And, again, there are blue regions above the red regions for passengers under 15 and between 30 & 40. We will re-affirm this using the age groups we created in a previous post.

In [7]:

ar_order = ['0-15', '16-29', '30-40', '41-59', '60+']
g = sns.barplot(x='AgeBin', y='Survived', data=k_trn, order=ar_order)

barplot of survival by binned age groups

And, the same picture. So, though age may not be the most informative feature, it probably should stay in our set of preferred model features.

For curiousity’s sake, lets have a look at Age by Pclass. I’ll use a boxplot for this one (practice, practice).

In [8]:

# compare age by travel class
sns.boxplot(x='Pclass',y='Age',data=k_trn,palette='tab10')

And, again, first class passengers tended to be older. Might be an indication of potential Age feature outliers. Something that may need to be considered/dealt with.

Like I said, lots of repetition possible.

Notice that the bottom half of 1st class and the top half of 2nd class is in that 30-40 range. Perhaps that’s why we saw better survival numbers for that age group. I.E. the passenger class they were in rather than their age.

Let’s see if we can sort that somehow.

In [9]:

s_ag_cl_1 = k_trn[k_trn["Survived"] == 1].groupby(["AgeBin", "Pclass"]).Survived.count().to_frame()
# s_ag_cl_1 = k_trn[k_trn["Survived"] == 1].groupby(["AgeBin", "Pclass"]).agg({'Survived': 'count'})
p_ag_cl_1 = k_trn[k_trn["Survived"] == 0].groupby(["AgeBin", "Pclass"]).Survived.count().to_frame()
# p_ag_cl_1 = k_trn[k_trn["Survived"] == 0].groupby(["AgeBin", "Pclass"]).agg({"Survived": 'count'})
p_ag_cl_1.rename(columns={'Survived':'Perished'}, inplace=True)
b_ag_cl_1 = pd.concat([s_ag_cl_1, p_ag_cl_1], axis=1)
display(b_ag_cl_1)

		Survived	Perished
AgeBin	Pclass
0-15	1	5	1.00
	2	19	NaN
	3	25	36.00
16-29	1	41	14.00
	2	32	45.00
	3	78	242.00
30-40	1	46	12.00
	2	23	31.00
	3	13	50.00
41-59	1	39	41.00
	2	12	18.00
	3	2	33.00
60+	1	5	12.00
	2	1	3.00
	3	1	4.00

That NaN in the Perished column forced the values to decimal rather than integer. I am at the moment too lazy to sort that out.

But looks like passenger class may have been a stronger influence in that 30-40 age group than age alone.

Fare

Now’s let’s have another look at the Fare feature.

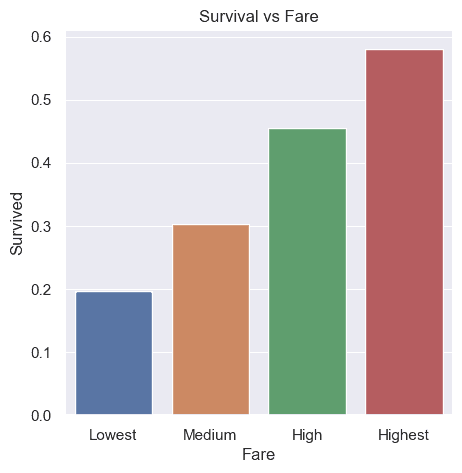
We have seen before that Fare appeared to have some correlation with survival. Here’s some code and a chart from an earlier post.

In [8]:

# categorize fares and plot against survival - let's just use the quartiles for now
f_cats = ['Lowest', "Medium", "High", "Highest"]
f_rngs = pd.qcut(k_trn["Fare"], len(f_cats), labels=f_cats)
fig, ax = plt.subplots(figsize=(5, 5))
p_ttl = ax.set_title("Survival vs Fare")
p_y = ax.set_ylabel("Survival Rate")
p_plt = sns.barplot(x=f_rngs, y=k_trn.Survived, ax=ax, ci=None)

swarmplot showing survival by gender and age

But we saw last post, that Pclass is strongly correlated with Fare. (Negatively correlated: I.E. 1st class fares generally higher that 3rd class fares.) Multicollinearity can cause problems with some machine learning algorithms. But, I don’t really know enough about that at this point. Something that might need looking into. That said, onwards and upwards.

In [10]:

# k_trn["FareBin"] = pd.cut(k_trn["Fare"], bins=5)
# g = sns.barplot(x="FareBin", y="Survived", data=k_trn)
fig, ax = plt.subplots(figsize=(30,6))
trn_survived = k_trn[k_trn["Survived"] == 1]
trn_perished = k_trn[k_trn["Survived"] == 0]
_ = sns.histplot(trn_survived["Fare"].dropna().values, bins=range(0, 300, 2), kde=False, color='blue')
_ = sns.histplot(trn_perished["Fare"].dropna().values, bins=range(0, 300, 2), kde=False, color='red')
_ = plt.xticks(rotation=25)
_ = plt.xlabel("Fare", weight='bold')

histplot of Fare versus survive or perish

Lower fares definitely reduce the likelihood of survival.

But big range. Let’s try using a log of the fare and see what we get.

In [11]:

# large range for fares, let's try using a log of fare
k_trn["logFare"] = np.log10(k_trn["Fare"].values + 1)
k_trn["logiFare"] = np.log10(k_trn["iFare"].values + 1)
fig, ax = plt.subplots(figsize=(30,6))
k_trn["logFareBin"] = pd.cut(k_trn["logFare"], bins=5)
g = sns.barplot(x="logFareBin", y="Survived", data=k_trn)

barplot, 5 bins, of log fare versus survival

Not sure about that drop in survival at the high end. But otherwise a somewhat linear increase in survival for the first 4 groups. Except that group 3 is only slightly more likely to survive than group 2.

When I reduced to just 4 groupings it was definitely a more linear increase without the drop at the end.

Let’s have a look at the log of iFare.

In [12]:

fig, ax = plt.subplots(figsize=(30,6))
k_trn["logiFareBin"] = pd.cut(k_trn["logiFare"], bins=5)
g = sns.barplot(x="logiFareBin", y="Survived", data=k_trn)

barplot, 5 bins, of log iFare versus survival

For the binned log of iFare, almost a linear trend except for bins 3 & 4 being pretty much equal.

All things considered, I will likely add feature with log of Fare or iFare or both to the dataset.

So, should I be using the logs for these fares rather than the fares themselves? Or should I be looking at using some form of normalization/scaling? Should I be binning the fares?

Just for fun, let’s use more bins.

In [14]:

# what about more bins
fig, ax = plt.subplots(figsize=(30,10))
k_trn["logiFareBin"] = pd.cut(k_trn["logiFare"], bins=10)
g = sns.barplot(x="logiFareBin", y="Survived", data=k_trn)

barplot, 10 bins, of log iFare versus survival

Hardly more linear, and some pretty large confidence intervals for a number of bins. But, I think we should look at adding log fares (total or individual) or some form of normalized values for one or both fare types.

Okay, let’s take a closer look at that correlation between Pclass and Fare.

In [14]:

fig = plt.figure(figsize=(15, 5))
_ = fig.subplots_adjust(left=None, bottom=None, right=None, top=None, wspace=0.3, hspace=0.5)
ax = fig.add_subplot(1, 2, 1)
ax = sns.boxplot(x="Pclass", y="Fare", hue="Survived", data=k_trn)
_ = ax.set_yscale("log")
ax = fig.add_subplot(1, 2, 2)
ax = sns.boxplot(x="Pclass", y="iFare", hue="Survived", data=k_trn)
_ = ax.set_yscale("log")

boxplots comparing Pclass vs Fare and iFare by survival status

iFare, individual fare estimate, has less variance within and better separation between classes.

Let’s look the kernel density estimation (KDEplot) of survival by fare within each passenger class, for both Fare and iFare.

In [15]:

k_all["logFare"] = np.log10(k_all["Fare"].values + 1)
k_all["logiFare"] = np.log10(k_all["iFare"].values + 1)

In [16]:

cols = 3
rows = 1
feature = "logFare"
lg_loc = ['upper left', 'upper left', 'upper right']
plt.style.use('seaborn-whitegrid')
fig = plt.figure(figsize=(20, 50))
rows = math.ceil(float(k_trn.shape[1]) / cols)
# define subplots
for i, pclass in enumerate(['Ist Class', '2nd Class', '3rd Class']):
  ax = fig.add_subplot(rows, cols, i + 1)
  df_subset = k_all[k_all['Pclass'] == i+1]
  g = sns.kdeplot(df_subset[feature][df_subset['Survived'] == 0].dropna(), shade=True, color="red")
  g = sns.kdeplot(df_subset[feature][(df_subset['Survived'] == 1)].dropna(), shade=True, color="blue")
  _ = g.set(xlim=(0, df_subset[feature].max()))
  _ = g.legend(['Perished', 'Survived'], loc=lg_loc[i])
  _ = plt.title(pclass)
  _ = ax.set_xlabel(feature, weight='bold')

In [17]:

cols = 3
rows = 1
feature = "logiFare"
lg_loc = ['upper left', 'upper left', 'upper left']
fig = plt.figure(figsize=(20, 50))
rows = math.ceil(float(k_trn.shape[1]) / cols)
# define subplots
for i, pclass in enumerate(['Ist Class', '2nd Class', '3rd Class']):
  ax = fig.add_subplot(rows, cols, i + 1)
  df_subset = k_all[k_all['Pclass'] == i+1]
  g = sns.kdeplot(df_subset[feature][df_subset['Survived'] == 0].dropna(), shade=True, color="red")
  g = sns.kdeplot(df_subset[feature][(df_subset['Survived'] == 1)].dropna(), shade=True, color="blue")
  _ = g.set(xlim=(0, df_subset[feature].max()))
  _ = g.legend(['Perished', 'Survived'], loc=lg_loc[i])
  _ = plt.title(pclass)
  _ = ax.set_xlabel(feature, weight='bold')

Fare does appear to have some predictive value within each class. Possibly providing more detail than Pclass alone.

A higher iFare doesn’t appear to improve the likelihood of survival. In fact for the two lower classes pretty much the opposite. Let’s look at fare by groupsize to see if anything pops out.

In [18]:

fig = plt.figure(figsize=(15, 5))
_ = fig.subplots_adjust(left=None, bottom=None, right=None, top=None, wspace=0.3, hspace=0.5)
ax = fig.add_subplot(1, 3, 1)
ax = sns.boxplot(x="Group", y="Fare", data=k_all[k_all['Pclass'] == 1])
_ = plt.title('1st Class')
ax = fig.add_subplot(1, 3, 2)
ax = sns.boxplot(x="Group", y="Fare", data=k_all[k_all['Pclass'] == 2])
_ = plt.title('2nd Class')
ax = fig.add_subplot(1, 3, 3)
ax = sns.boxplot(x="Group", y="Fare", data=k_all[k_all['Pclass'] == 3])
_ = plt.title('3rd Class')

boxplots of group size versus fare by passenger class

In [19]:

fig = plt.figure(figsize=(15, 5))
_ = fig.subplots_adjust(left=None, bottom=None, right=None, top=None, wspace=0.3, hspace=0.5)
ax = fig.add_subplot(1, 3, 1)
ax = sns.boxplot(x="Group", y="iFare", data=k_all[k_all['Pclass'] == 1])
_ = plt.title('1st Class')
ax = fig.add_subplot(1, 3, 2)
ax = sns.boxplot(x="Group", y="iFare", data=k_all[k_all['Pclass'] == 2])
_ = plt.title('2nd Class')
ax = fig.add_subplot(1, 3, 3)
ax = sns.boxplot(x="Group", y="iFare", data=k_all[k_all['Pclass'] == 3])
_ = plt.title('3rd Class')

boxplots of group size versus iFare by passenger class

Fare generally increases with group size. Not so iFare. Which does make sense since iFare normalizes out the impact of group size.

And, in 3rd class, there is a downward trend in iFare for group sizes of up to 4. Likely/maybe due to fare discounts for families in that passenger class. Similar trend for group sizes of 3 and 4 in 2nd class. And, family/group sizes of 2 to 4 did seem to have a higher likelihood of survival.

Done?

This has turned into another lengthy post, so I think I am going to call it quits and take a break for an hour, or day, or two. Not sure if I am going to continue with this extended EDA, try a few new scoring runs or look at “science based” feature selection. Just so you know, leaning toward the last of those alternatives.

Feel free to download and play with my version of this post’s related notebook.

Resources

pandas.DataFrame.copy
pandas.get_dummies
Using Python to Find Correlation Between Categorical and Continuous Variables
seaborn.FacetGrid
seaborn.histplot
seaborn.kdeplot
Seaborn Bar Plot Ordering
Visualizing distributions of data (link is for section on kernel density esitmation)